數學在我們周圍，它以無數的方式塑造了我們對世界的了解。它為現在塑造世界做出了貢獻，并幫助人們克服了各種正常的問題。下面提出的是一些數學方程，它們明確地改變了我們所知道的世界。

1)畢達哥拉斯定理

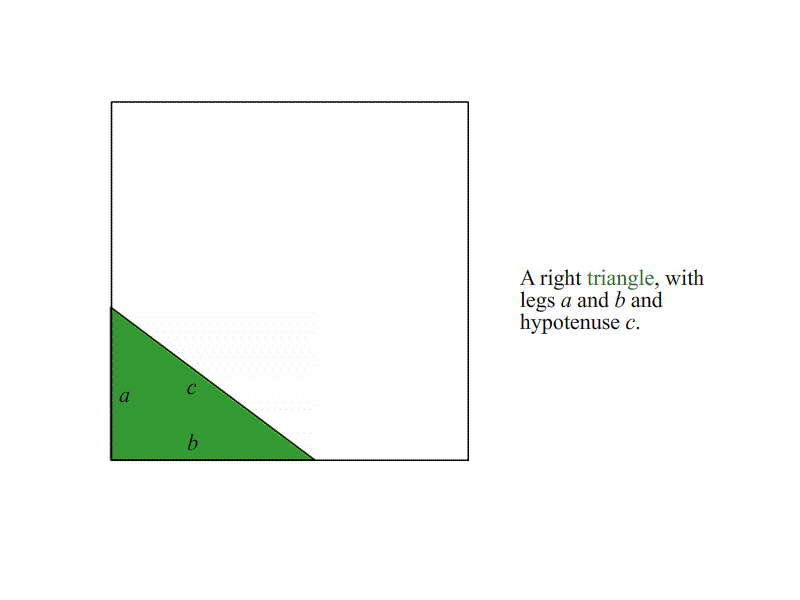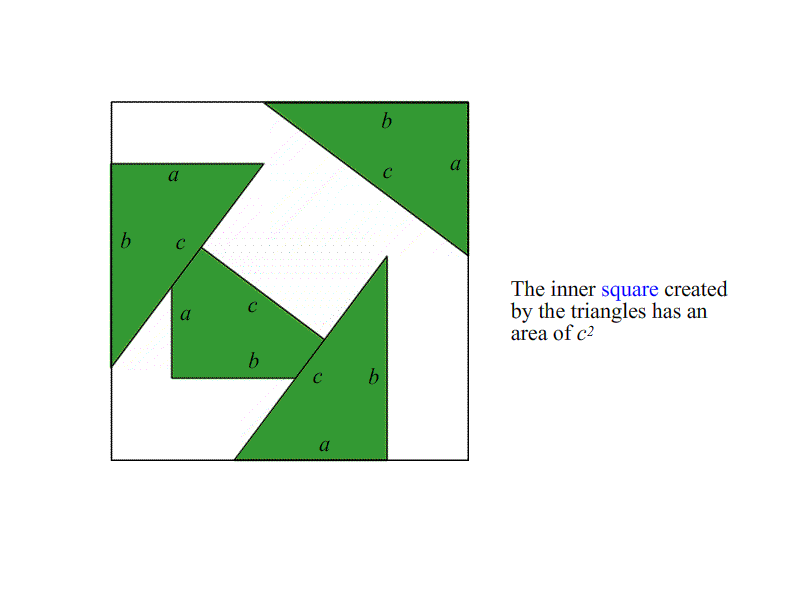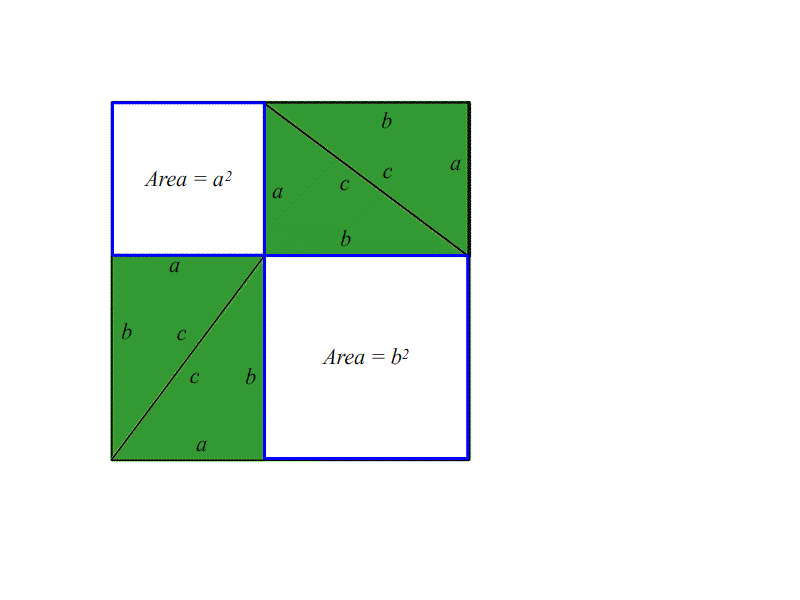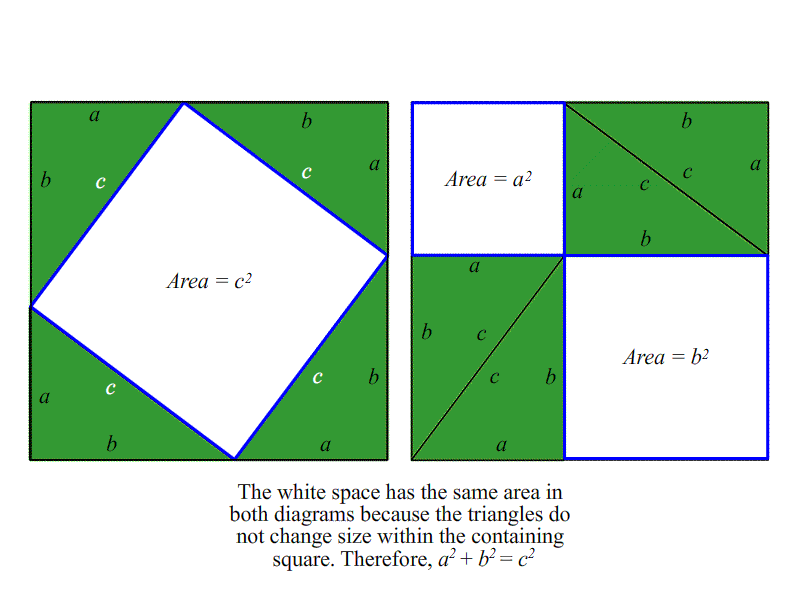
這個定理是我們對幾何學理解的基礎。它描述了平面上直角三角形的側面之間的關系：將短邊的長度a和b平方，將它們加在一起，并得到長邊長度的平方，c。

2)對數

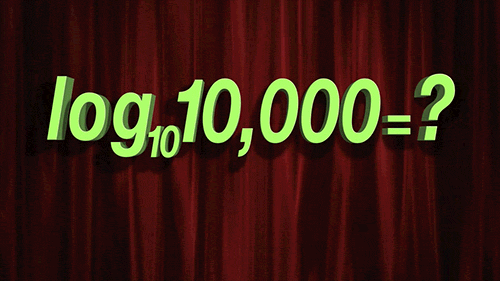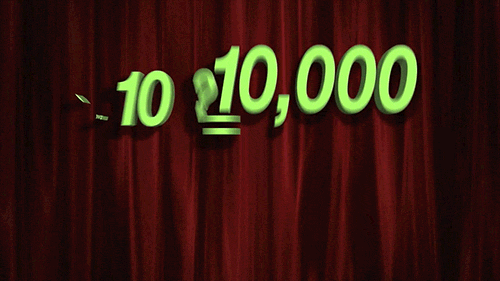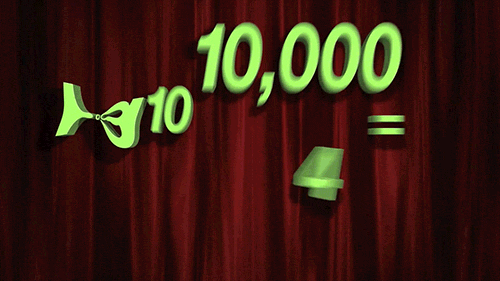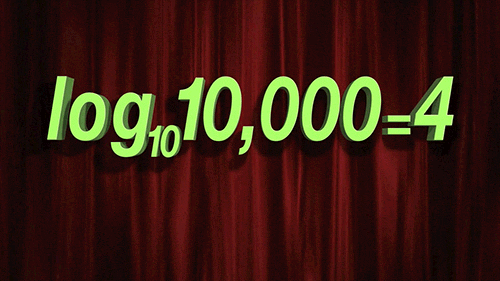
對數是指數函數的反轉或對立。一個數字的對數是一個指數，其中另一個固定值，即基數必須被提高以產生該數字。直到數字計算機的發展，這是快速繁殖大量的最常見的方法，大大加快了物理，天文學和工程學的計算。

3)微積分

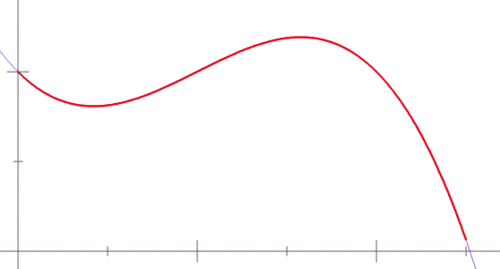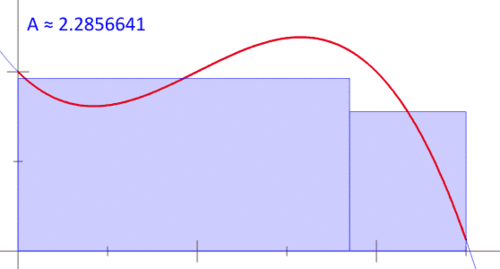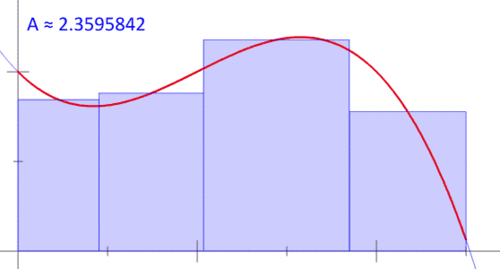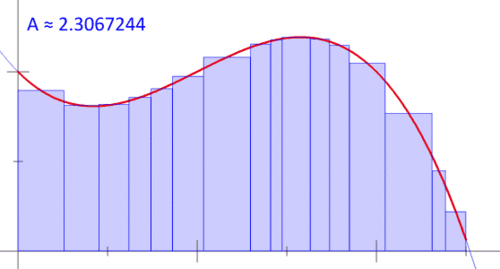
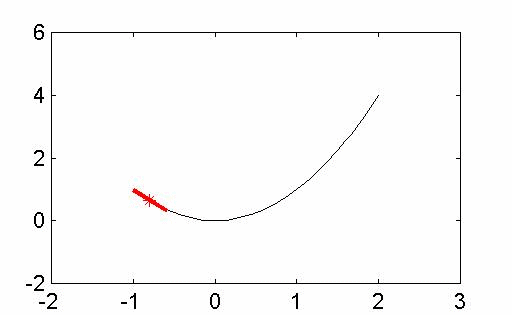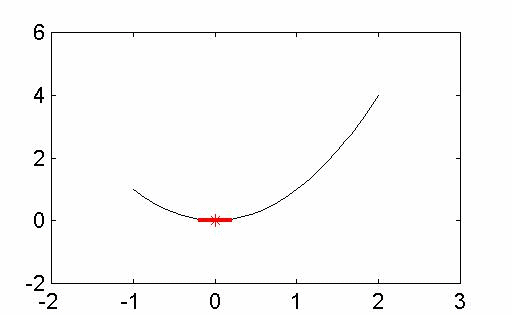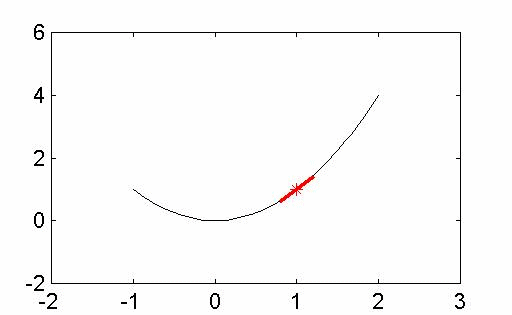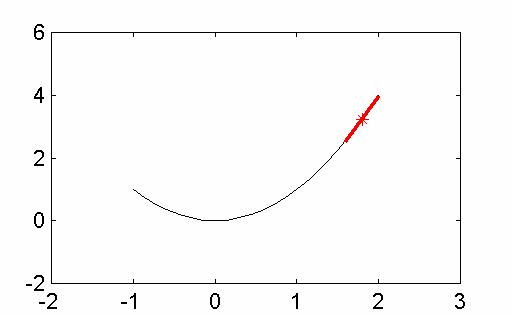
當然，很多科學都有興趣了解事情的變化，而衍生和積分是數學家和科學家們理解變化的核心。第一個動畫顯示中點雷曼和，以近似曲線下的面積。第二個動畫顯示兩個函數的偏導數，z = f(x，y)。

4)重力定律

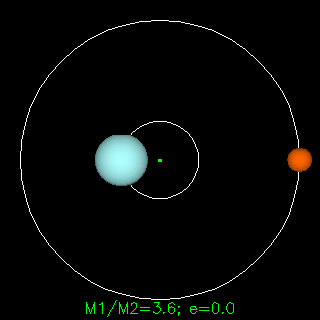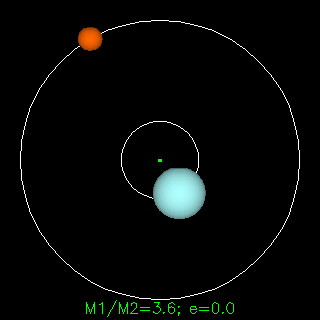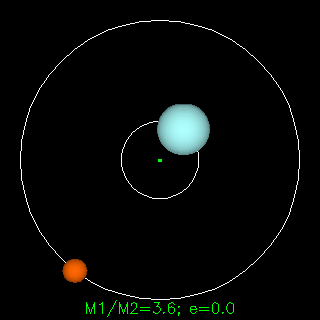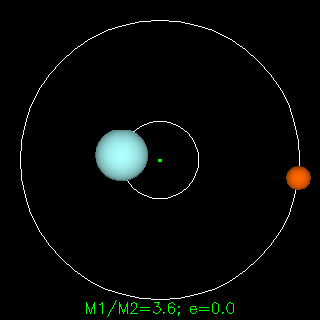
牛頓的引力定律描述了兩個物體之間的重力F，以通用常數G，兩個物體的質量m1和m2以及物體之間的距離r表示。牛頓定律是一個非凡的科學歷史 - 幾乎完全可以解釋為什么行星按照自己的方式進行。牛頓說，他的重力法適用于任何兩個具有大量物體的物體 - 它適用于地球上的任何動作，以及空間中的任何動作。

5)歐拉公式多面體

多面體是多邊形的三維版本。歐拉公式表示，只要您的多面體表現良好，如果您將頂點和面組合在一起，并減去邊緣，則總是會得到2.無論多面體是否具有4,8,12,20 ，或任何數量的面孔。

6)傅里葉變換

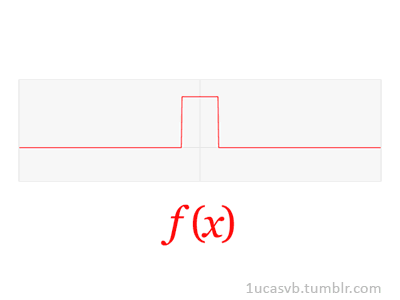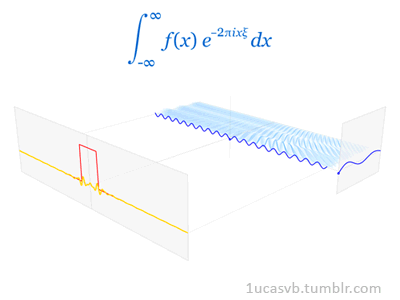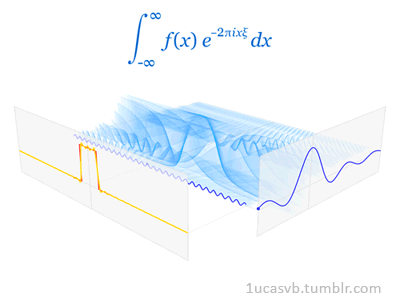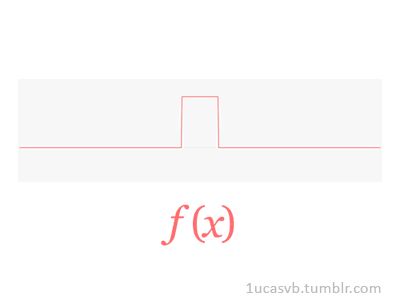
它是用于在時域和頻域之間轉換信號的數學變換，其在物理和工程中具有許多應用。

7)正態分布

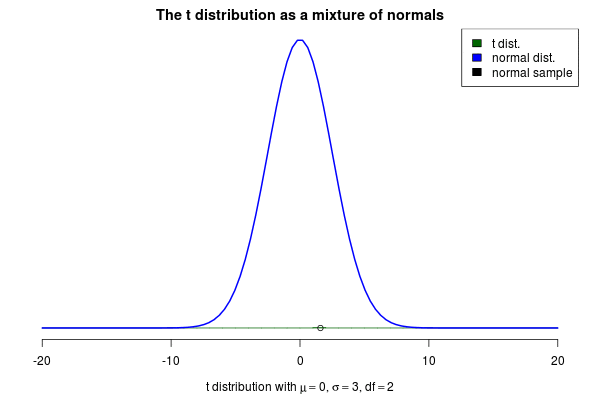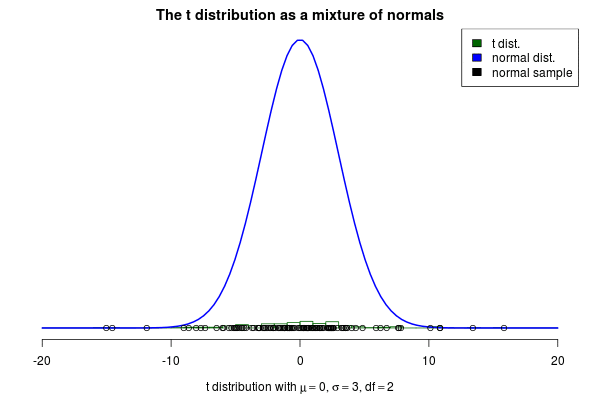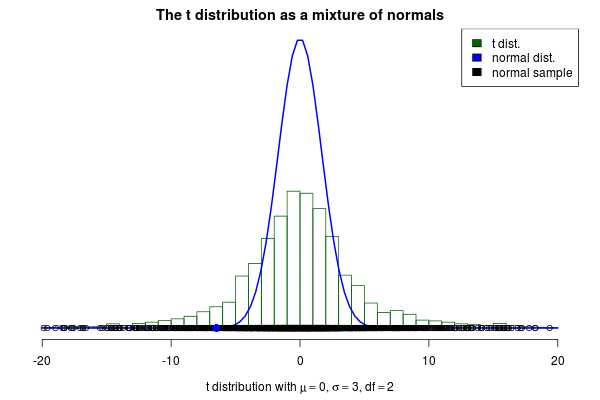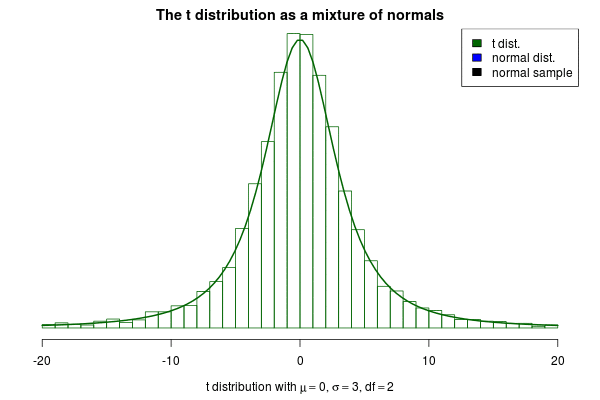
正常曲線用于物理，生物學和社會科學，以模擬各種屬性。正常曲線經常出現的一個原因是它描述了大群獨立過程的行為。

8)波動方程

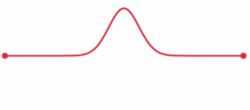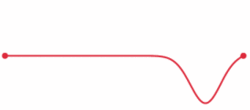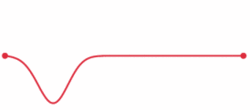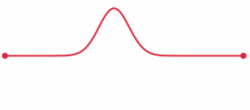
這是一個微分方程，或者一個方程，描述一個財產如何隨著時間的推移而變化。波浪方程描述了波浪的行為 - 一個振動的吉他弦，拋石頭后的池塘中的波紋，或從白熾燈出來的光。

9)麥克斯韋方程

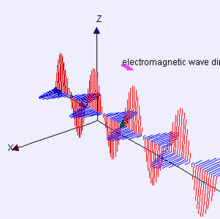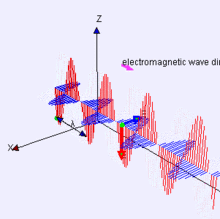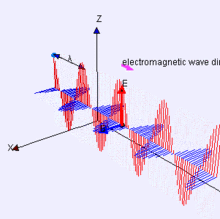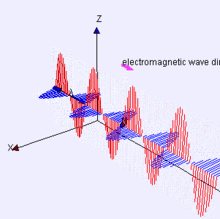
這組四個微分方程描述了電(E)和磁(H)之間的行為和關系。麥克斯韋方程是我們解釋電磁學在日常規模上如何工作的基礎。

10)熱力學第二定律

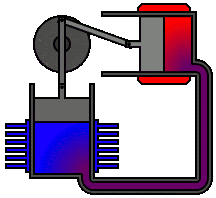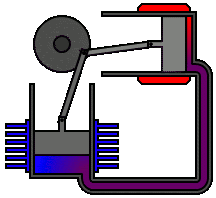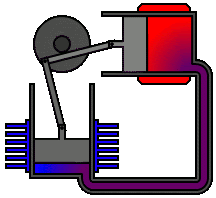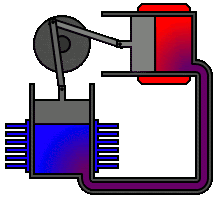
第二個熱力學定律表明，孤立系統的熵不會降低，因為孤立的系統總是朝向熱力學平衡發展，即具有最大熵的狀態。動畫顯示了一種被稱為熱力學第二定律的Alpha型斯特林引擎。

11)相對論

經典方程E = mc2表示物質和能量彼此相等。狹義相對性帶來的想法，如光的速度是一個普遍的速度限制，時間的流逝是不同的人以不同的速度移動。

12)薛定er方程

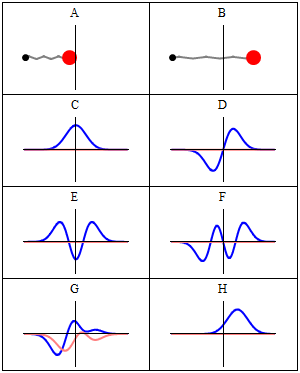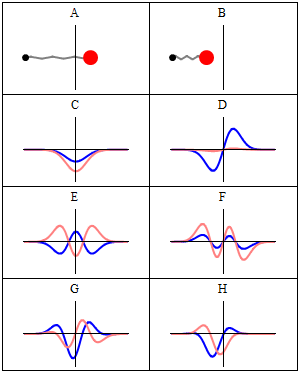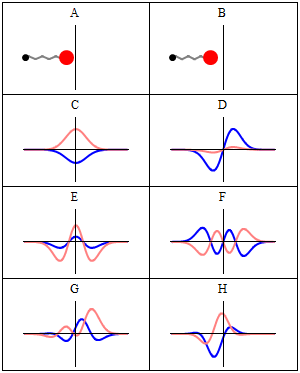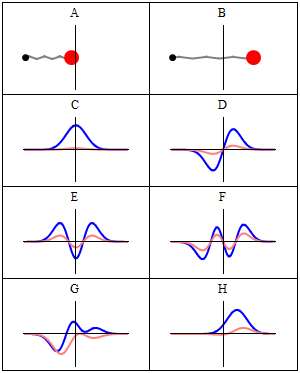
這是量子力學中的主要方程。由于廣義相對論以其最大尺度解釋了我們的宇宙，這個方程式決定了原子和亞原子粒子的行為。大多數現代技術還需要量子力學 - 核能，基于半導體的計算機和激光器都圍繞量子現象構建。動畫顯示經典力學(A-B)和量子力學(C-H)中的A諧波振蕩器。在(A-B)中，附著在彈簧上的球來回振蕩。(C-H)是這種情況下薛定er方程的六個解。

13)混沌理論

這個方程是一個邏輯圖。它描述了一個通過時間發展的過程 - xt + 1，下一個時期的一些數量x的水平由右邊的公式給出，它取決于xt，現在的水平x。k是選定的常數。對于k的某些值，地圖顯示混沌行為：如果我們從x的某個特定初始值開始，則過程將以一種方式演化，但如果我們從另一個初始值開始，即使是非常接近第一個值，過程將以完全不同的方式發展。
如果你想了解塑料的微觀世界，就上搜料網。